جواب حل فعالیت صفحه ۴۵ و ۴۶ ریاضی دهم انسانی

جواب فعالیت صفحه ۴۵ ریاضی دهم انسانی ، پاسخ حل فعالیت صفحه ۴۵ ریاضی دهم انسانی ، پاسخ فعالیت صفحه ۴۶ ریاضی دهم انسانی ، جواب صفحه ۴۵ ریاضی دهم انسانی ، توضیح فعالیت صفحه ۴۶ ریاضی دهم انسانی

جواب فعالیت صفحه ۴۵ ریاضی دهم انسانی

1- کدام‌یک از رابطه‌ها که با نمودار پیکانی نمایش داده شده‌اند، تابع‌اند؟ چرا؟

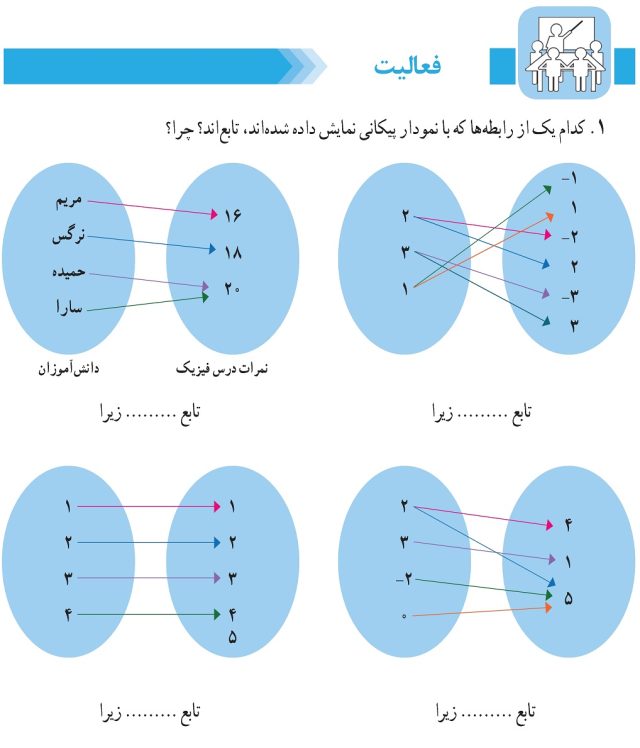
تابع نیست، زیرا هر عضو مجموعه سمت چپ با دو عضو از مجموعه سمت راست مناظر است. مثلا ۲ با ۲- و۲

تابع است، زیرا هر عضو مجموعه سمت چپ با یک عضو از مجموعه سمت راست متناظر است

تابع نیست، زیرا عدد ۲ با دو عدد از مجموعه سمت راست (۴ و ۵) متناظر است

تابع است، زیرا هر عضو مجموعه سمت چپ با یک عضو از مجموعه سمت راست متناظر است

2- کدام مجموعه از زوج مرتب‌ها، نمایش یک تابع است؟

F= {(2,3),(3,3),(4,3),(5,3)} (الف

تابع است

G= {(4,1),(2,−1),(1,−1),(4,2)} (ب

تابع نیست

H= {(2,3)} (پ

تابع است

I= {(3,3)} (ت

تابع است

J= {(1,1),(2,2),(3,3),(2,4)} (ث

تابع نیست

3- کدام‌یک از رابطه‌ها که نمودار مختصاتی آنها رسم شده است، تابع‌اند؟ چرا؟

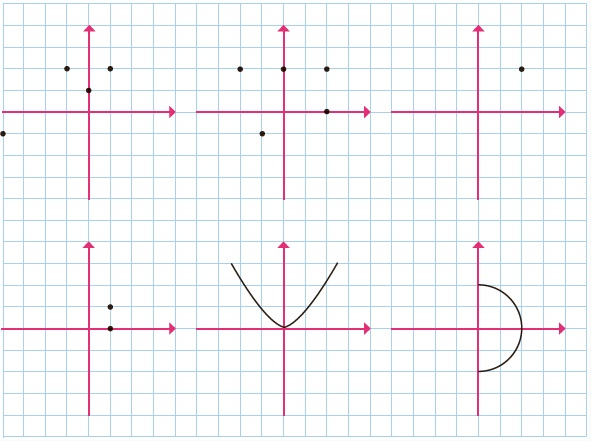
بالا سمت راست ؛ تابع است، زیرا تنها یک عضو دارد.

بالا وسط : تابع نیست، زیرا به ازای 2 = * y برابر دو مقداره و ۲ خواهد بود.

بالا سمت چپ : تابع است، زیرا هر عضو از مقادیر X (محور طولها) با یک عضو از مقادیر لا (محور عرض ها) متناظر است

پایین سمت راست : تابع نیست، زیرا به ازای 0 = y x برابر دو مقدار ۲- و ۲ خواهد بود.

پایین وسط:تابع است، زیرا هر عضو از مقادیر X (محور طولها) با یک عضو از مقادیر y (محور عرض ها) متناظر است

پایین سمت چپ: تابع نیست، زیرا به ازای 1 = Xه و برابر دو مقدار ۲- و ۲ خواهد بود

4- کدام یک از رابطه‌های تعریف شدهٔ زیر، تابع است و کدام تابع نیست؟ دلایل خود را بنویسید.

الف) رابطه‌ای که به هر شهر در ایران، سوغاتیِ آن شهر را نسبت می‌دهد. تابع است / تابع نیست

تابع نیست زیرا یک شهر ممکن است چندین نوع سوغاتی داشته باشد.

ب) رابطه‌ای که به هر فرد، روز تولد او را نسبت می‌دهد. تابع است / تابع نیست

تابع است زیرا هر فرد یک روز تولد دارد.

پ) رابطه‌ای که به هر شهر، نمایندهٔ آن شهر در مجلس شورای اسلامی را نسبت می‌دهد. تابع است / تابع نیست

پ) تابع نیست زیرا ممکن است یک شهر چند نماینده داشته باشد

ت) رابطه‌ای که به هر مسلمان، قبلهٔ او را نسبت می‌دهد. تابع است / تابع نیست

تابع است زیرا هر مسلمان یک قبله دارد.

با توجّه به فعالیت قبل و تعریف تابع می‌توان گفت:

– اگر رابطهٔ بین x و y را (x متغیر مستقل) به‌صورت جدولی و زوج مرتبی نمایش دهیم، در صورتی تابع است که هیچ دو زوج مرتب متمایزی با مؤلفه‌های اول برابر در آن وجود نداشته باشد.
– اگر رابطه از مجموعهٔ A به مجموعه‌ی B را با نمودار پیکانی نمایش دهیم، در صورتی این رابطه تابع است که از هر عضو A دقیقاً یک پیکان خارج شود.
– اگر نمودار مختصاتی یک رابطه رسم شود، در صورتی این رابطه تابع است که هیچ دو نقطه‌ای روی خطی که موازی محور yها باشد، قرار نگیرند.